2014年杭州市第二次高考科目教學質量檢測
一、選擇題(本大題共 10 小題,每小題 5 分,共 50 分.在每小題給出的四個選項中,只有一項是
符合題目要求的.)
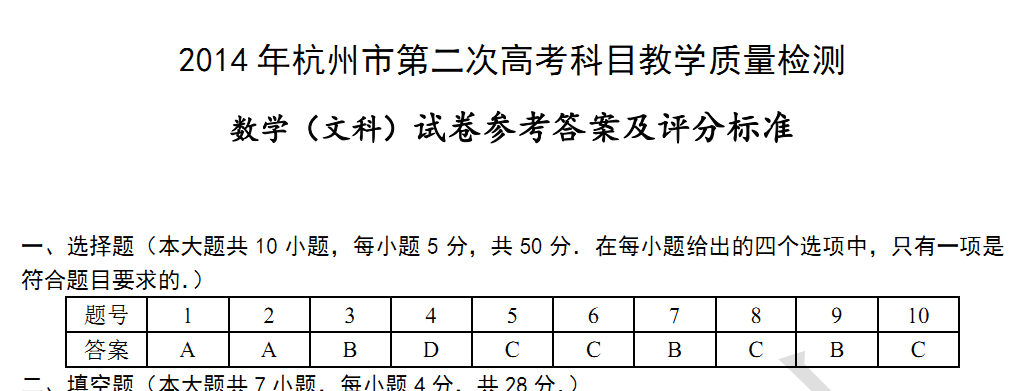
題號 1 2 3 4 5 6 7 8 9 10
答案 A A B D C C B C B C
二、填空題(本大題共7小題,每小題 4分,共28分.)
11.-1-i 12.an=2n
13.
28
3
14.
1
2
15.[0,4] 16.直線 17.
1
8
三、解答題: 本大題共5小題, 共72分.解答應寫出文字說明, 證明過程或演算步驟.
18. (本題滿分14分)
解: (Ⅰ)設等差數列的公差為 d,等比數列的公比為q,
則a1=1,a2=2,a3=1+d,a4=2q,a5=1+2d,
所以4+d=2q,(1+d)+(1+2d)=2+2q,
解得 d=2,q=3.
所以
1
2
, ( 2 1)
2 3 ,( 2 )
n n
n n k
a
nk
,k∈N*.
……………………………………………………………………7 分
(Ⅱ)S2n=
(1 2 1) 2(1 3 )
2 1 3
n
nn
=n2
-1+3n
. ………………………………7分
19. (本題滿分14分)
解:(Ⅰ)因為S△ABC=
1
2
acsinB,所以
1
2
×3sinB=
33
4
,
即
sinB=
3
2
,
又因為 0<B<π,所以 B=
π
3
或
2π
3
.………………………………………7分
(Ⅱ)由(Ⅰ)可知,B=
π
3
或
2π
3
,
當B=
π
3
時,因為
a2
+c
2
-ac=(a+c)
2
-3ac=2,ac=3,
所以 a+c=
11
;
當B=
2π
3
時,因為
a2
+c
2
+ac=2,ac=3,
所以
a2
+c
2
=-1(舍去) .
所以△ABC的周長為 a+c+b=
11
+
2
.…………………………7 分
20. (本題滿分15分)
解: (Ⅰ)取AC的中點F,連接 DF,A′F,
則DF//AB,A′E//AB,
所以DF//A′E.
又因為DF=
1
2
AB,A′E=
1
2
AB,
所以DF=A′E.
所以四邊形DFA′E 是平行四邊形.
所以ED//A′F,又A′F
平面ACC′A′,
所以ED//平面ACC′A′. ………………………………………5 分
(Ⅱ)由題意,AD⊥BC,AD⊥CC′,BC∩CC′=C,
所以 AD⊥平面BB′C′C.
又因為 B′D
平面BB′C′C,C′D
平面BB′C′C,
所以 AD⊥B′D,AD⊥C′D.
所以 ∠B′DC′即是二面角B′-AD-C′的平面角.
在△B′DC′中,得
B′D=
32
,C′D=
32
,B′C′=
22
,
所以
cos∠B′DC′=
2 2 2
2
BD CD BC
BD CD
=
7
9
.
……………………………………………………………………10分
數學學習 http://www.gzdwyxj888.com/math/